The data's in. (And let me digress for a moment by turning from one passion, number theory, to another, the English language - whether that be the British or American variety. I will never say "the data are in" - this is a linguistic vulgarity. "The statistics are...", yes, but data is a collective noun singular. That it happens to have a virtually unused singular, datum, does not excuse the plural use of data. It is no more a plural noun than "information" is. Do you hear people say the "information are"...? I hope not, but that is how tin-eared "data are" sounds to me. It's not English!* )

As I was saying, the data is in. And the data says there appear to be an infinite number of paired primes for every even - and only even - quadratic interval (QI). If you're not sure what I mean by a paired prime - no, I do not mean twin prime - you must read my previous column about it. I have found that commonly occurring paired primes are not limited to ones separated by the equivalent of exactly 2 QIs (the span of 3 perfect squares), as discussed previously.

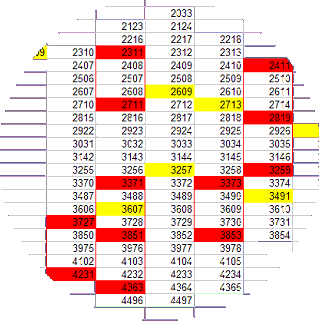
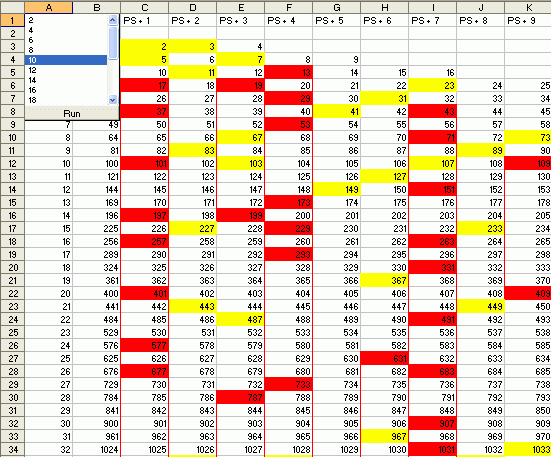
There are, in fact, high numbers of paired primes for every even multiple of the quadratic interval: 2, 4, 6, 8, 10, through 100, through 1000, and so on. For simplicity and clarity, I will refer to paired primes of any particular quadratic interval as Q-Paired Primes (QPPs), using a number representing how many intervals the pairs span: QPP-<n>. So QPP-250 would be the designation for paired primes that span 250 quadratic intervals.

You will have a much clearer idea of what I mean by paired if you run the Excel VBA code provided below. However, the screenshot to the right shows some QPP-4s. To take just one pair-prime example from this: 2311 is offset by 7 from perfect square 2304; 2711 is offset by 7 from perfect square 2704.

I hear you say: "So what? Of course you should be able to find primes at the same locations in various quadratic intervals...." But wait and consider the following:

• The locations are not relative; they are absolute. They are ordinal offsets from preceding perfect squares.
• The highest concentrations of paired primes do not occur for the lowest even quadratic interval - namely, 2. In fact, QI-2 ranks 221st out of the first 500 even intervals for paired-prime frequency. (QI-210 ranks highest among the first 500.)
• Since the quadratic interval is growing at f(x) = Θ(x2), the fact that the mean frequency of these pairings diminishes only very gradually as we approach pairs spanning 1,000 quadratic intervals - greater than 1 million at a minimum - is a notable result. Also notable is the steadiness of the frequency fluctuation.

Data for this chart can be downloaded (8KB)

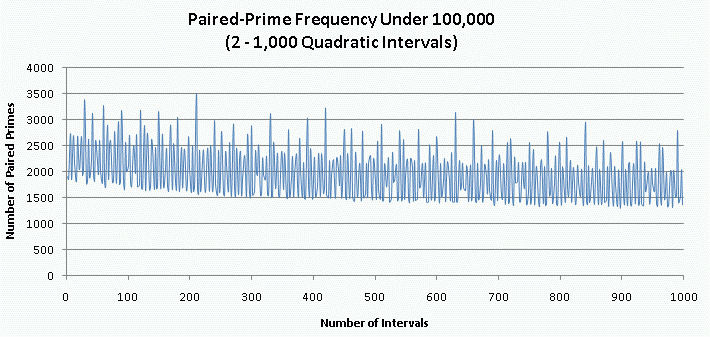
Of the 500 even intervals under 1000, the 10 with the highest paired-prime frequency are as follows:

Quadratic Intervals	Paired Primes (<100,000)
210	3496
30	3380
60	3269
420	3213
120	3172
90	3167
150	3147
630	3137
330	3116
42	3112

 

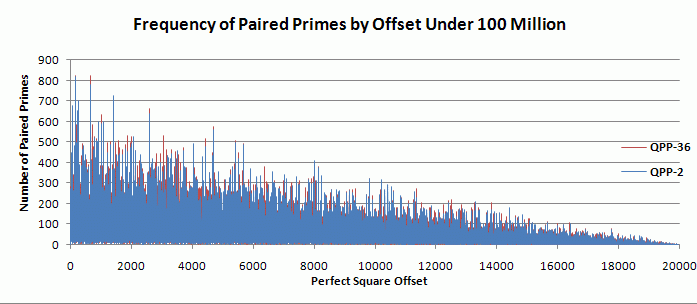
The following graph looks at the frequency of paired primes by offset for all numbers under 100 million. The graph shows data for two intervals: QPP-2 and QPP-36 are superimposed, showing the closeness of the distribution for each one.

Data for this chart can be downloaded: QPP-2 (119KB) , QPP-36 (179KB)

There is a striking correspondence in the 10 offsets that yield the highest number of paired primes for each interval:

Strangely, this is the case even though there is a big difference in the number of offsets producing paired primes for each interval. For QPP-2, there are 12,992 different offsets on which paired primes occur; for QPP-36, there are 19,484 - 67% more paired-prime-producing offsets. The aggregate number of pairs under 100 million is 31,746 for QPP-2 and 31,645 for QPP-36.

Visualizing Paired Primes

I have improved the Excel visualization of paired primes in a number of ways from the original column on biquadratic paired primes:

• It now shows both odd and even offsets.
• It does not repeat numbers.
• It allows you to choose prime-pair quadratic intervals (from 2 to 36) from a list.

(All this functionality is packed into fewer than 100 lines of code - which says more about the effectiveness of VBA for Excel than my programming powers!)

Zoomed out, it looks like this for QPP-10.

All you have to do is to select everything in the text area below and drag or copy it to the Excel Visual Basic Editor, dropping it into the VBAProject ThisWookbook object. Save and exit the file. Then reopen it, and the code will autostart providing that your macro security is not high or very high. When execution stops, change intervals from the selection list in the top left corner and click Run.

VBA Code for Excel:

Public lb as Object Private Sub Workbook_Open() With Worksheets(1) For sc = 1 To .Shapes.Count .Shapes(sc).Select Selection.Cut sc = sc - 1 If sc = 0 Then Exit For Next Set lb = .Shapes.AddFormControl(xlListBox, 0, 0, 95, 90) For QIs = 2 To 36 Step 2 lb.ControlFormat.AddItem QIs Next lb.ControlFormat.ListIndex = 1 Set bt = .Shapes.AddFormControl(xlButtonControl, 0, 90, 95, 15) bt.Select bt.Name = "Button1" Selection.Caption = "Run" .Cells(1, 1).Select ActiveSheet.Shapes("Button1").OnAction = "ThisWorkbook.ChangeInterval" .Cells.ClearContents .Cells.ClearFormats End With Rotations End Sub Private Sub ChangeInterval() Worksheets(1).Cells.ClearFormats Rotations End Sub Public Sub Rotations() Dim QuadIntvs As Integer With Worksheets(1) .Cells(1, 1).Value = "Rotation" .Cells(1, 2).Value = "Perfect Square" QuadIntvs = lb.ControlFormat.List(lb.ControlFormat.ListIndex) Offset = 1 For cl = 3 To 256 .Cells(1, cl).Value = "PS + " + Str$(Offset) Offset = Offset + 1 Next Rotation = 1 Do Until Rotation > 200 perfectsquare = Rotation * Rotation 'perfect square diffsquare = (perfectsquare - previoussquare) 'diff between this psq and previous psq nextperfectsquare = (Rotation + 1) * (Rotation + 1) PR = Rotation + 2 .Cells(PR, 1).Value = Str$(Rotation) 'A .Cells(PR, 2).Value = Str$(perfectsquare) 'B ec = 0 For Offset = 1 To 253 ec = ec + 1 If perfectsquare + Offset > nextperfectsquare Then Exit For .Cells(PR, 2 + ec).Value = Str$(perfectsquare + Offset) If IsPrime(perfectsquare + Offset) Then If .Cells(PR, 2 + ec).Interior.Color <> vbRed Then .Cells(PR, 2 + ec).Interior.Color = vbYellow End If QR = ((Rotation + QuadIntvs) * (Rotation + QuadIntvs)) + Offset If IsPrime(QR) Then .Cells(PR, 2 + ec).Interior.Color = vbRed .Cells(PR + QuadIntvs, 2 + ec).Interior.Color = vbRed For rt = 0 To QuadIntvs - 1 .Cells(PR + rt, 2 + ec).Borders(xlEdgeLeft).Color = vbRed .Cells(PR + rt, 3 + ec).Borders(xlEdgeLeft).Color = vbRed Next End If End If DoEvents Next DoEvents Rotation = Rotation + 1 previoussquare = perfectsquare DoEvents Loop End With MsgBox "Finished. You can select another Interval and click Run.", vbInformation End Sub Private Function IsPrime(pt As Variant) As Boolean Dim ff As Variant If pt <> 2 Then If ModOp(pt, 2) = 0 Then IsPrime = False Exit Function End If For ff = 3 To Sqr(pt) Step 2 DoEvents If ModOp(pt, ff) = 0 Then IsPrime = False Exit Function End If Next End If IsPrime = True End Function Private Function ModOp(value1 As Variant, Value2 As Variant) As Double Dim vratio As Variant vratio = CDec(value1) / CDec(Value2) ModOp = CDec(vratio) - Int(vratio) End Function

 

Michael M. Ross

Please let me know if you've seen this relationship or an analogous one described elsewhere.